Crittografia post-quantistica: tra minacce concrete e opportunità rivoluzionarie
Al Forum ICT Security 2025, Daniele Venturi dell’Università Sapienza traccia la roadmap di una rivoluzione crittografica già in corso. Quando il quantum computing diventerà realtà, i nostri sistemi di sicurezza attuali potrebbero crollare in pochi istanti. Ma la sfida quantistica nasconde anche opportunità straordinarie che cambieranno per sempre il modo in cui proteggiamo i dati.
L’intervento del professor Daniele Venturi, ordinario presso il Dipartimento di Informatica dell’Università di Roma Sapienza, ha aperto uno squarcio sul futuro della cybersecurity nell’era quantistica. Durante la 23ª edizione del Forum ICT Security, tenutosi a Roma il 19-20 novembre 2025, il relatore ha presentato un quadro complesso dove minacce e opportunità si intrecciano, delineando scenari che vanno ben oltre la semplice sostituzione degli algoritmi crittografici attuali.
Il titolo dell’intervento, “Crittografia (Post-)Quantistica: Sfide ed Opportunità”, racchiude già la duplice natura della rivoluzione in corso: da un lato la necessità urgente di proteggere i sistemi esistenti, dall’altro le straordinarie possibilità tecnologiche che le nuove assunzioni matematiche ci offrono.
Il paradigma della sicurezza dimostrabile: le fondamenta della crittografia moderna
“La crittografia moderna si basa su quello che chiamiamo il paradigma della sicurezza dimostrabile”, ha esordito Venturi, richiamando le pietre miliari poste da Shafi Goldwasser e Silvio Micali negli anni Ottanta. L’idea fondamentale è avere una prova matematica rigorosa della sicurezza di un crittosistema, non basarsi solo su intuizioni o test empirici.
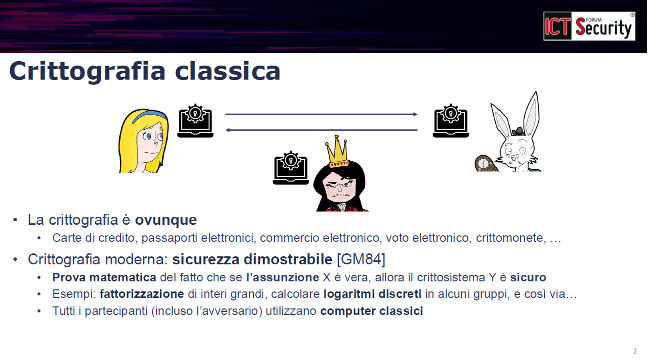
Il primo passo è definire con precisione cosa significa che un cifrario o uno schema di firma è sicuro. Una volta stabilita la definizione, si procede alla dimostrazione matematica, che può avvenire in due modalità: incondizionata (è vera sempre, punto) oppure condizionata a specifiche assunzioni matematiche.
“Violare la sicurezza del sistema diventa equivalente a violare l’assunzione X”, ha spiegato l’esperto. Gli esempi classici di queste assunzioni sono la difficoltà computazionale di fattorizzare grandi numeri interi o calcolare logaritmi discreti in gruppi finiti: problemi su cui generazioni di matematici si sono arrovellate per centinaia di anni senza trovare algoritmi efficienti.
Questa solidità matematica ci rende sicuri: se esistesse un attacco efficace contro RSA o altri sistemi, avremmo automaticamente scoperto come fattorizzare numeri interi rapidamente, il “Santo Graal” della teoria dei numeri che i matematici inseguono da secoli.
L’algoritmo di Shor: quando la minaccia quantistica diventa concreta
In questo scenario consolidato irrompe la computazione quantistica. L’algoritmo di Shor, presentato da Peter Shor nei primi anni Novanta, ha dimostrato che un calcolatore quantistico sufficientemente potente può fattorizzare numeri interi e risolvere il problema del logaritmo discreto in tempo polinomiale – una velocità che renderebbe inutili gran parte dei sistemi crittografici attuali.
“Fattorizzare un intero di 1.024 bit richiede circa 2.050 qubit logici e miliardi di gate quantistici”, ha precisato Venturi, sottolineando che siamo ancora molto lontani da questo obiettivo tecnologico. Il record attuale di implementazione reale dell’algoritmo di Shor è la fattorizzazione del numero 21, senza progressi significativi negli ultimi dieci anni.
Eppure il NIST (National Institute of Standards and Technology) statunitense ha già avviato e in gran parte completato il processo di standardizzazione dei crittosistemi resistenti agli attacchi quantistici. Il motivo di questa apparente urgenza? Il principio precauzionale sintetizzato nell’espressione inglese “better safe than sorry” (meglio prevenire che curare).
“Gli attacchi quantistici potrebbero già stare avvenendo in questo momento”, ha ammonito il relatore con tono grave. “Un attaccante potrebbe raccogliere oggi grandi quantità di dati cifrati per decifrarli domani, quando i computer quantistici saranno finalmente disponibili”. Uno scenario noto come “harvest now, decrypt later” (raccogli ora, decifra poi) che rende urgente la migrazione verso algoritmi post-quantistici anche prima che i computer quantistici operativi esistano.
Post-quantistica versus quantistica: una distinzione cruciale
Lo speaker ha tenuto a chiarire una distinzione fondamentale, spesso confusa nel dibattito pubblico e nelle comunicazioni commerciali.

Nella crittografia post-quantistica, Alice e Bob (mittente e destinatario, secondo la nomenclatura classica) utilizzano computer tradizionali e scambiano messaggi classici attraverso canali di comunicazione standard. Tuttavia, devono proteggersi da un avversario che dispone di un computer quantistico. Il requisito minimo è quindi sfruttare assunzioni matematiche basate su problemi che rimangono difficili da risolvere anche per calcolatori quantistici.
Nella crittografia quantistica, invece, tutti i partecipanti – Alice, Bob e potenzialmente anche l’avversario – dispongono di capacità quantistiche. La comunicazione può avvenire tramite stati quantistici, i messaggi possono essere codificati in qubit, e le chiavi crittografiche stesse possono essere stati quantistici. Questa tecnologia sfrutta i principi fondamentali della fisica quantistica per realizzare applicazioni completamente impossibili nel mondo classico.
“La distinzione è cruciale”, ha sottolineato Venturi, “perché confondere i due ambiti porta a fraintendimenti sulle capacità reali e sui limiti delle tecnologie disponibili”.
Learning with Errors: la matematica dietro i nuovi standard
Per illustrare le basi matematiche della crittografia post-quantistica, il professore ha presentato uno dei problemi fondamentali alla base dei nuovi standard NIST: il problema Learning with Errors (LWE), letteralmente “apprendimento con errori”.
Si tratta essenzialmente di risolvere un sistema di equazioni lineari modulari (equazioni in aritmetica modulo un certo numero primo q) che sono state perturbate aggiungendo del “rumore” casuale con una specifica distribuzione statistica. Normalmente, se si dispone di un numero sufficiente di equazioni, un sistema lineare è sempre risolvibile in modo efficiente con gli algoritmi studiati nei corsi universitari di algebra lineare.
“Ma quando queste equazioni sono perturbate da rumore con una certa distribuzione, il problema diventa computazionalmente difficile da risolvere”, ha spiegato Venturi. Sotto specifiche condizioni parametriche e certe assunzioni matematiche, questo problema diventa equivalente ad alcuni classici problemi sui reticoli (lattice problems) che i matematici studiano da decenni senza aver trovato algoritmi efficienti – né classici né quantistici.
“Congetturiamo che questi algoritmi efficienti non esistano”, ha aggiunto il relatore, “ed è proprio su questa congettura che fondiamo la sicurezza dei nuovi crittosistemi post-quantistici”.
L’opportunità nascosta: la cifratura omomorfa
Ma ecco la svolta inaspettata, l’aspetto che ha acceso l’entusiasmo del relatore. “Queste nuove assunzioni matematiche, oltre ad aprire la porta a sistemi sicuri in ambito post-quantistico come quelli standardizzati dal NIST, ci permettono di realizzare forme completamente nuove di strumenti crittografici che prima erano impensabili”.

Una di queste tecnologie rivoluzionarie è la cifratura omomorfa (fully homomorphic encryption), ovvero la capacità di eseguire calcoli arbitrari su dati cifrati senza mai doverli decifrare.
Il caso d’uso è illuminante: “Immaginate di cifrare un messaggio e inviarlo al cloud. Volete che il cloud calcoli una funzione sui vostri dati, ma non volete rivelargliela in chiaro per questioni di privacy. Come può il cloud operare su dati che non può vedere?”
La risposta sembra quasi magica. Il cloud, conoscendo solo la chiave pubblica, la descrizione della funzione da calcolare e i dati cifrati, applica un algoritmo speciale e produce un nuovo ciphertext (testo cifrato). Quando il proprietario dei dati lo decifra con la propria chiave privata, ottiene esattamente il risultato della funzione applicata ai dati originali – senza che il cloud abbia mai “visto” i dati in chiaro.
“Questa era una delle domande aperte più grandi e affascinanti nella crittografia a chiave pubblica fin dalla sua invenzione negli anni Settanta”, ha ricordato Venturi. Ron Rivest, uno degli inventori dell’algoritmo RSA, parlava già dei cosiddetti “privacy homomorphisms”. Alcuni crittosistemi classici come RSA o ElGamal soddisfano parzialmente questa proprietà, ma solo per operazioni molto ristrette (ad esempio la moltiplicazione): moltiplicando due ciphertext si ottiene un ciphertext che decifra al prodotto dei due plaintext originali.
“Quello che vogliamo fare è realizzare questa proprietà per tutte le funzioni computabili, non solo per operazioni elementari”, ha precisato il relatore. Questo problema è rimasto aperto per oltre trent’anni, fino a quando Craig Gentry, allora dottorando a Stanford, lo ha risolto nel 2009 con una costruzione basata proprio su problemi legati ai reticoli.
Il progresso da allora è stato rapidissimo. Oggi esistono librerie software che implementano schemi di cifratura omomorfa basati su LWE e su varianti correlate, con prestazioni che si avvicinano all’utilizzabilità pratica per applicazioni reali – dal calcolo su dati medici sensibili all’elaborazione di informazioni finanziarie nel cloud.
Offuscamento dei programmi: il codice che custodisce i propri segreti
Un’altra opportunità rivoluzionaria emersa dallo studio delle assunzioni post-quantistiche riguarda l’offuscamento dei programmi (program obfuscation).
La domanda di ricerca è tanto semplice quanto profonda: “È possibile che un programma mantenga i propri segreti anche quando il codice eseguibile sta fisicamente nelle mani di un attaccante, senza fare affidamento su alcun hardware fidato (trusted hardware)?”
L’esempio più immediato è un programma che contiene una password e la confronta con l’input dell’utente. Normalmente, per proteggere la password, si memorizza solo il suo hash crittografico, accettando l’input solo se il suo hash corrisponde. Ma per programmi più complessi questo approccio non è sufficiente.
L’obiettivo dell’offuscamento è creare una versione trasformata del programma originale che: (1) calcoli esattamente la stessa funzione dell’originale, (2) sia completamente incomprensibile, (3) non riveli alcuna informazione sui segreti incorporati nel codice, come password, chiavi crittografiche o logiche di business proprietarie.
“Questa tecnologia ha portato a una vera e propria rivoluzione nel mondo accademico della crittografia negli ultimi dieci anni”, ha sottolineato Venturi con enfasi. “Permette di costruire applicazioni crittografiche che erano completamente sconosciute in tutta la storia precedente della disciplina”.
La sfida aperta? “Costruire l’offuscamento dei programmi basandosi soltanto su LWE rimane ad oggi uno dei problemi aperti più importanti della crittografia teorica”. Le costruzioni esistenti richiedono assunzioni matematiche molto più forti e controverse rispetto a LWE, il che ne limita la fiducia e l’applicabilità pratica.
La trappola delle dimostrazioni: il riavvolgimento quantistico
Il professore ha poi affrontato un aspetto tecnico cruciale, spesso trascurato anche da esperti del settore: la transizione alla sicurezza post-quantistica non si limita a sostituire le assunzioni matematiche di base.
“L’illusione è che basti rimpiazzare l’assunzione con una variante resistente al quantistico e il gioco è fatto. Purtroppo non è così”, ha avvertito Venturi. “Anche le definizioni di sicurezza e le tecniche di dimostrazione devono essere compatibili con la presenza di avversari quantistici”.
L’esempio tecnico del riavvolgimento quantistico (quantum rewinding) illumina il problema. Molte dimostrazioni di sicurezza nella crittografia classica utilizzano una tecnica chiamata “riavvolgimento”: durante la dimostrazione matematica, si considera l’algoritmo dell’avversario e lo si “riavvolge” a uno stato precedente per analizzarne il comportamento.
Se l’avversario è un algoritmo classico, questa operazione è perfettamente lecita e non modifica il modello di calcolo. Ma se l’avversario dispone di un computer quantistico, “riavvolgendolo” si perturba inevitabilmente il suo stato quantistico interno, e l’avversario quantistico “se ne accorge” perché le leggi della fisica quantistica impediscono di copiare o riavvolgere stati quantistici sconosciuti senza disturbarli.
Questo effetto fa letteralmente “crollare” molte dimostrazioni di sicurezza classiche quando si tenta di applicarle al contesto quantistico. “È necessario intervenire con tecniche più sofisticate per estendere quelle dimostrazioni e renderle valide contro avversari quantistici”, ha spiegato il relatore.
“Questa è una misconception diffusa: non basta utilizzare assunzioni post-quantistiche. Bisogna verificare attentamente anche quali garanzie di sicurezza vengono fornite e come sono costruite le prove matematiche che le supportano”.
Quantum Key Distribution: promesse teoriche e limiti pratici
Passando alla crittografia quantistica vera e propria – quella dove anche gli utenti legittimi sfruttano tecnologie quantistiche – Venturi ha analizzato criticamente la Quantum Key Distribution (QKD), ovvero la distribuzione quantistica delle chiavi crittografiche.
La QKD sfrutta le leggi fondamentali della fisica quantistica, in particolare il principio che misurare uno stato quantistico lo perturba inevitabilmente, per permettere ad Alice e Bob di condividere una chiave segreta su un canale di comunicazione completamente insicuro e potenzialmente intercettato.
La buona notizia? “Nel mondo classico, condividere una chiave su un canale insicuro richiede assolutamente assunzioni computazionali, come la difficoltà della fattorizzazione. Non si può fare in maniera incondizionata, nemmeno per proteggere solo da intercettazioni passive. Nel mondo quantistico invece è possibile ottenere sicurezza incondizionata – garantita dalle leggi della fisica, non da congetture matematiche”.
Inoltre, non sono necessari computer quantistici universali completi: “Bastano tecnologie più accessibili come la comunicazione in fibra ottica con fotoni singoli o collegamenti da satellite”, ha precisato il relatore.

Le cattive notizie, però, sono sostanziali. “Purtroppo la maggior parte dei fotoni non riescono ad arrivare da Alice a Bob, e questo effetto peggiora in modo esponenziale con la distanza”. Le attenuazioni tipiche nelle fibre ottiche limitano drasticamente la portata operativa.
I numeri parlano chiaro: il record mondiale è 511 chilometri di distanza con un bit rate di 3,37 bit al secondo. “È una velocità assolutamente bassissima, praticamente inutilizzabile per applicazioni reali”, ha commentato con realismo il professore.
Il problema si aggrava ulteriormente considerando che la vera sicurezza incondizionata richiede l’uso del cifrario di Vernam (o one-time pad), dove la chiave deve essere lunga esattamente quanto il messaggio da cifrare. “Questo è un limite inerente delle leggi dell’informatica: non si può fare di meglio. Quindi 3,37 bit al secondo per generare chiavi che devo poi usare per cifrare messaggi della stessa lunghezza… il conto non torna per usi pratici”.
I sistemi ibridi: un compromesso inevitabile
La soluzione pratica attualmente perseguita sono i sistemi ibridi QKD che combinano la distribuzione quantistica delle chiavi con cifrari simmetrici veloci come AES.
Lo schema funziona così: la QKD genera periodicamente chiavi condivise tra Alice e Bob, seppur a basso bit rate. Queste chiavi vengono poi utilizzate come input per cifrari a blocchi standard (come AES) che permettono di cifrare messaggi a velocità normale, praticamente illimitata. Le implementazioni più avanzate di sistemi ibridi raggiungono ad esempio 66 kilobit al secondo a 70 chilometri di distanza.
Ma qui Venturi ha inserito un’osservazione pungente che smonta gran parte della retorica commerciale sulla QKD: “A quel punto, però, potete ottenere esattamente lo stesso risultato con poche centinaia di righe di codice software, usando una Key Derivation Function (KDF) crittografica e AES”.
Lo schema alternativo classico funziona così: Alice e Bob condividono inizialmente una chiave segreta K (magari scambiata con un protocollo di key exchange tipo Diffie-Hellman post-quantistico). Poi utilizzano una KDF per generare da K una sequenza di chiavi derivate K₁, K₂, K₃… indipendenti tra loro, che usano con AES per cifrare i messaggi successivi. “Nessun dispositivo quantistico costoso, nessun limite di distanza ai 511 chilometri, nessun problema di attenuazione”.
L’unico vantaggio della QKD? “Se un attaccante compromette fisicamente l’intero dispositivo di Alice o Bob, con la soluzione classica perde tutta la sicurezza. Con la QKD mantieni alcune garanzie”. Ma anche questo vantaggio può essere ottenuto, ha notato il relatore, “al prezzo di utilizzare tecniche più complesse che sfruttano assunzioni post-quantistiche, come i sistemi basati su LWE”.
La conclusione implicita è chiara: i benefici pratici della QKD rispetto ad alternative post-quantistiche puramente software sono molto più limitati di quanto il marketing tecnologico lasci intendere.
Monete quantistiche: il denaro digitale non clonabile
Guardando al futuro post-computer quantistico, il relatore ha presentato due applicazioni affascinanti ma ancora lontane dalla realizzazione pratica.
Le monete quantistiche (quantum money) sfruttano uno dei principi fondamentali della meccanica quantistica: il teorema del no-cloning, che stabilisce che stati quantistici sconosciuti non possono essere copiati perfettamente. “Se gli stati quantistici non sono clonabili, posso usarli come banconote digitali?” La domanda, posta per la prima volta decenni fa, è brillante nella sua semplicità.
Il problema fondamentale del denaro digitale classico è infatti proprio la facilità di duplicazione: copiare un file è banale, quindi come impedire il double spending (la doppia spesa della stessa “banconota” digitale)? Le criptovalute come Bitcoin risolvono il problema con registri distribuiti (blockchain), ma richiedono infrastrutture complesse e consumano enormi quantità di energia.
“Con le monete quantistiche, la fisica stessa impedisce la clonazione. È un’idea geniale”, ha ammesso Venturi con entusiasmo. Purtroppo l’implementazione pratica è estremamente complicata.
Le uniche costruzioni funzionanti finora sono schemi “a chiave privata” (secret-key quantum money), dove per verificare l’autenticità di una moneta è necessario contattare direttamente l’ente che l’ha emessa. “Questo ovviamente non scala: è come dover chiamare la Banca Centrale ogni volta che qualcuno vuole verificare una banconota”.
Quello che servirebbe sono monete quantistiche a chiave pubblica (public-key quantum money), dove chiunque possa verificare autonomamente l’autenticità di una moneta quantistica senza dover contattare l’emittente. “Questo è molto, molto, molto più complicato da realizzare”, ha sottolineato il professore. “Esistono tantissimi tentativi falliti e una bellissima linea di ricerca attiva che studia questo problema, ma ad oggi rimane un problema aperto per essere risolto in maniera efficiente”.
Copyright protection quantistico: l’antipirateria definitiva
L’ultima applicazione futuristica presentata è la protezione quantistica del copyright (quantum copy protection), che affronta il problema della pirateria software.
L’idea, proposta dal fisico teorico Scott Aaronson nel 2009, è ancora una volta elegantemente semplice: “Se posso associare uno stato quantistico a un programma software, riesco a impedirne la copia illegale sfruttando il teorema del no-cloning?”
Nel mondo classico si usa il watermarking digitale: un marchio incastonato nel codice che tutti possono verificare ma che è difficile da rimuovere senza danneggiare il programma. È un deterrente contro la pirateria, non una protezione assoluta.
La protezione quantistica promette di più, ma ha limiti intrinseci. “Purtroppo è impossibile per programmi learnable“, ha spiegato Venturi. Se un programma è sufficientemente semplice da poter essere “imparato” sottoponendogli varie query di test e osservandone gli output, allora una volta imparato può comunque essere replicato, indipendentemente dalla protezione quantistica.
“Quindi questa forma di protezione funziona inerentemente solo per programmi complessi, non facilmente apprendibili tramite interrogazioni”. Ma il problema è che per questi programmi complessi “la protezione quantistica del copyright sembra implicare matematicamente l’esistenza di monete quantistiche a chiave pubblica”. E come abbiamo visto, quelle non sappiamo ancora costruirle efficientemente.
“Sembra anche implicare l’offuscamento dei programmi, un altro problema aperto”, ha aggiunto. Esistono costruzioni per sottoclassi ristrette di programmi, sotto assunzioni matematiche molto forti, ma nulla di pratico o generale.
Conclusioni: tra realismo e lungimiranza strategica

Nelle note conclusive, Venturi ha mantenuto un equilibrio sapiente tra entusiasmo per le possibilità future e realismo sullo stato attuale della tecnologia.
“C’è sempre la barzelletta nel settore: sono già vent’anni che il computer quantistico ‘uscirà tra cinque anni'”, ha scherzato il professore suscitando risate in platea. “Però staremo a vedere. La ricerca avanza, gli investimenti crescono, i progressi ci sono. Non sappiamo quando, ma probabilmente accadrà”.
Le conclusioni pratiche per i professionisti della sicurezza informatica sono chiare:
Sui crittosistemi post-quantistici: “Esistono già, sono basati su problemi che rimangono difficili anche per computer quantistici, e per le applicazioni crittografiche principali l’efficienza è ormai comparabile a quella delle soluzioni classiche attuali”. La transizione è quindi tecnicamente fattibile e va pianificata seriamente.
Sulle opportunità: “La cosa che spero di avervi comunicato è che utilizzare questo tipo di assunzioni matematiche apre nuovi orizzonti nel mondo della crittografia. Permette di realizzare applicazioni molto interessanti – come la cifratura omomorfa – che potranno essere utilizzate nel mondo classico, indipendentemente poi dallo sviluppo o meno dei computer quantistici”. La minaccia quantistica ha paradossalmente accelerato la scoperta di nuove possibilità crittografiche.
Sulla Quantum Key Distribution: qui il tono è diventato più critico. “I crittosistemi quantistici possono dare la possibilità di fare cose completamente impossibili nel mondo classico, come la QKD senza assunzioni computazionali. Però attenzione: brevi distanze, bit rate limitatissimo, e soprattutto è possibile in pratica solo se abbandoniamo la sicurezza incondizionata – che è l’unico aspetto veramente interessante e distintivo della QKD“.
“Questo aspetto è spesso trascurato nelle presentazioni commerciali e risulta in affermazioni esagerate sulle capacità reali della QKD”, ha ammonito il relatore con franchezza.
Sulle applicazioni futuristiche: “Le applicazioni più sorprendenti come le monete quantistiche e la protezione quantistica del copyright richiedono capacità computazionali quantistiche che sono ancora molto lontane dall’essere realizzate praticamente”.
Un intervento che ha saputo bilanciare rigore tecnico e visione strategica, evitando sia il catastrofismo sulla minaccia quantistica sia l’entusiasmo acritico per tecnologie ancora immature. La rivoluzione quantistica non è solo una minaccia da cui difendersi, ma anche – e forse soprattutto – un’opportunità storica per ripensare radicalmente i paradigmi fondamentali della sicurezza informatica e della protezione dei dati.
“Rimaniamo sintonizzati”, ha concluso Venturi con un sorriso. La partita è appena iniziata.
Guarda il video completo dell’intervento:

Daniele Venturi è Professore Ordinario presso il Dipartimento di Informatica dell'Università di Roma Sapienza, dove dirige il Laboratorio SCRYPTO dal 2016. La sua ricerca si focalizza sulla crittografia teorica ed applicata.







