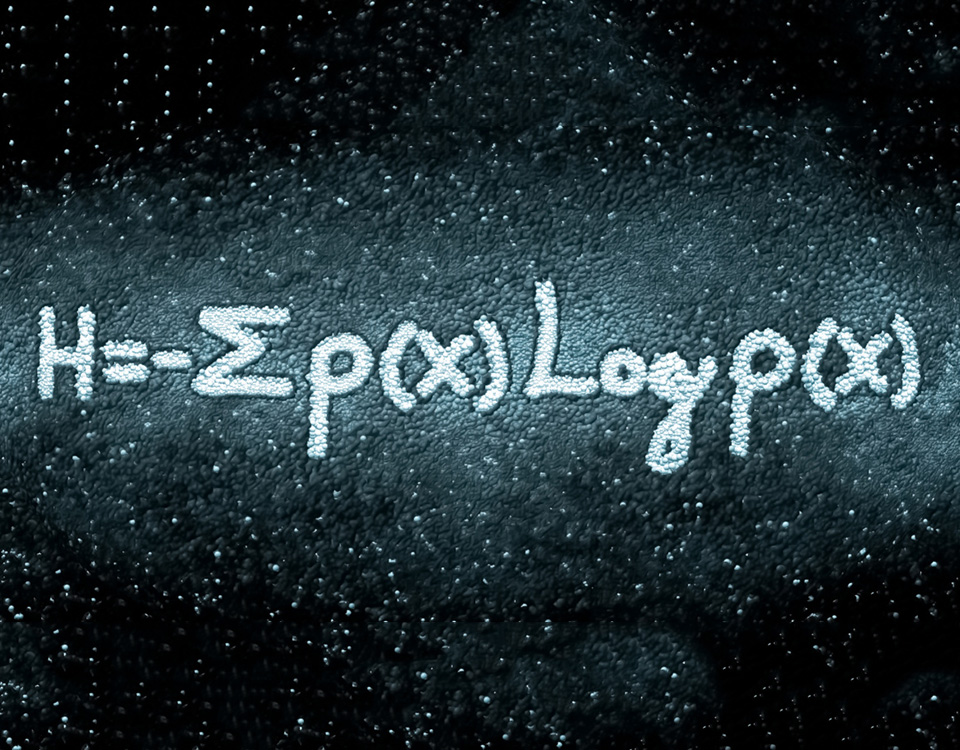Entropia e sicurezza
Il calcolo del livello di entropia nell’analisi di un malware, o di un file binario in generale, rappresenta il primo passo da eseguire, in quanto aiuta a determinare la natura del file e – di conseguenza – quale strada seguire e quali metodi utilizzare per analizzarlo.
Il termine venne introdotto in termodinamica all’inizio del XIX secolo. Solo nel 1948, nel suo A Mathematical Theory of Communication, Claude Shannon ha definito l’entropia nel campo dell’information theory.
Per meglio comprendere quanto segue, occorre conoscere la definizione del temine in relazione all’ICT. Semplificando, l’entropia misura il grado di casualità di un sistema. In particolare, in un file, l’entropia misura quanto sono disordinati i byte che lo compongono. Può quindi essere considerata come la misura del grado di disordine di un determinato insieme di dati, disordine inteso come variazione del valore del singolo byte.
Vediamo un esempio: innanzitutto produciamo i file da analizzare. Creiamo un file riempito con valori uguali e uno con valori casuali.
$ head -c 1M < /dev/zero > zero-example $ head -c 1M < /dev/urandom > random-example
$ ent zero-example Entropy = 0.000000 bits per byte. $ ent random-example Entropy = 7.999811 bits per byte.
Come si può vedere da questo semplice test, l’entropia risulta essere bassa se il file è lineare e massima se il contenuto del file è completamente casuale.
Quando è utile
Fin qui tutto bello e interessante, però la domanda sorge spontanea: come può aiutare tutto ciò?
Per rispondere a questa domanda è necessaria una piccola premessa: nelle operazioni di sicurezza, soprattutto nel reverse engineering, ci troviamo di fronte due tipi di aree con particolare entropia, prodotti dalle operazioni di compressione e crittografia.
Quando abbiamo a che fare con un file binario, ci capita spesso di incontrare aree sconosciute nella forma e nel comportamento: in questi casi è utile almeno conoscerne la natura.
Quindi, in una fase esplorativa, prima di un’analisi statica, sono utili anche strumenti statistici e di data visualization per determinare a grandi linee il tipo di software. In questa ottica sono utili il calcolo e la visualizzazione dell’entropia, per determinare la tipologia delle varie aree del file in esame e scegliere il giusto approccio da seguire.
Ispezionando il diagramma dell’intero file, è possibile identificare come sono organizzate le varie aree e individuare il loro grado di interesse nell’analisi. In genere, le aree contenenti codice hanno un’entropia maggiore delle aree non contenenti codice (i dati tipicamente hanno bassa entropia, in quanto sono spesso ripetitivi).
Ad esempio, analizzando il file test.bin con binwalk -E abbiamo:
$ binwalk -E test.bin DECIMAL HEXADECIMAL ENTROPY -------------------------------------------------------------------------------- 0 0x0 Falling entropy edge (0.748507) 352256 0x56000 Rising entropy edge (0.992041) 1875968 0x1CA000 Rising entropy edge (0.992091) 2285568 0x22E000 Falling entropy edge (0.365989) 2457600 0x258000 Rising entropy edge (0.990475) 12689408 0xC1A000 Falling entropy edge (0.249381)
e l’immagine in Figura 1.
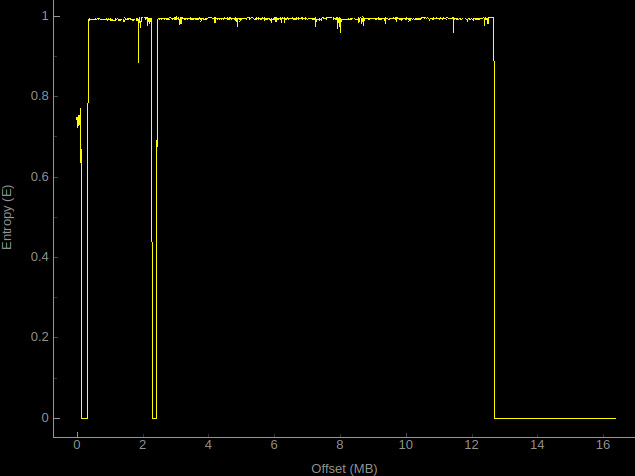
Determinata l’entropia delle varie zone dobbiamo chiederci essenzialmente due cose: perché quell’area ha un entropia del genere e di conseguenza cosa c’è in quell’area.
Entropia dei file binari
Come detto, misurare l’entropia di un file binario aiuta a capire se il file è stato cifrato o compresso. Il metodo più comune per determinarne i livelli in un file è l’entropia di Shannon.
La formula di Shannon (Riquadro 1) va da 0 a 8: un valore basso indica che il file non ha subito nessun offuscamento, viceversa un valore alto sta ad indicare la presenza di un’operazione di cifratura o compressione.
In dettaglio: i file “puliti” generalmente hanno un valore inferiore a 5, i file compressi hanno valori superiori a 5 ma inferiori a 6 (dipende molto dal tipo di compressione, ad esempio un’area compressa con LZMA avrà, da questo punto di vista, un comportamento molto simile ad un’area cifrata, sono quindi necessarie ulteriori indagini) e infine i file cifrati hanno un’entropia maggiore di 6. Ovviamente questa misura ci dice solo indicativamente che un file abbia subito una determinata procedura.
Per calcolare l’entropia sono utili strumenti come la risorsa online binvis.io oppure binwalk -E o ancora ent.ent (A Pseudorandom Number Sequence Test Program) che, oltre ad essa, ci fornisce altre grandezze utili durante l’analisi di un file. In particolare ci interessano la distribuzione Chi Quadrato e il Monte Carlo Value for Pi che ci danno informazioni sulla natura del file. Per le definizioni e il significato relativo ad un file, rimando alla pagina ufficiale del progetto: fourmilab.ch/random/.
Con ent avremo un output del genere:
$ ent test.bin Entropy = 7.371475 bits per byte. Optimum compression would reduce the size of this 4194304 byte file by 7 percent. Chi square distribution for 4194304 samples is 24956388.61, and randomly would exceed this value less than 0.01 percent of the times. Arithmetic mean value of data bytes is 107.9100 (127.5 = random). Monte Carlo value for Pi is 3.273785852 (error 4.21 percent). Serial correlation coefficient is 0.312169 (totally uncorrelated = 0.0).
Riquadro 1: Entropia di Shannon
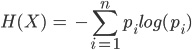
Questa (in figura) è data dal valore negativo della sommatoria di p(i), che rappresenta la probabilità di ogni elemento i del file, moltiplicato per il logaritmo della probabilità di i. La parte della formula all’interno della sommatoria è sicuramente quella più importante: assegna un valore alto agli eventi rari e un valore basso agli eventi più comuni.
Conclusioni
Da quanto detto finora si deduce che, in fase di analisi statica, è buona norma calcolare l’entropia soprattutto quando abbiamo a che fare con un oggetto non identificato. Inoltre va sottolineato che tale concetto ci viene incontro non solo quando dobbiamo fare delle operazioni di reverse engineering, ma anche quando facciamo un penetration test o siamo alla ricerca di bug.
Articolo a cura di Gianluigi Spagnuolo

Si interessa di reverse engineering, attualmente si occupa della sicurezza dei firmware.
Collabora con diverse riviste del settore scrivendo di programmazione e sicurezza.